regression_multiple

[ Ein Psychologe steigt schnaufend in ein Taxi. Der Taxifahrer: "Na, wohin soll es den gehen?" Der Psychologe: "Fahren Sie mich irgendwo hin, ich werde überall gebraucht." ]

Modul "Multivariate Statistik": Multiple Regression

Uwe Mattler, Peter Zezula

Ziel ist es, Regressionsanalysen mit mehr als einem Prädiktor rechnen und visualisieren zu können.
Ausserdem sollen Sie Techniken zur Prädiktoren-Auswahl kennenlernen und die Güte der Anpassung beurteilen lernen.

 

Multiple Regression

Vorgehensschema

stark orientiert an der entsprechenden Wikipedia-Seite

Situation klären (Design, Variablen, Skalenniveau etc.)

Datenaufbereitung

Visueller Überblick empfehlenswert

Verfahren auswählen (Struktur, v. a. Skalenniveau entscheidend)

Modell aufstellen

Modellanpassung

• Koeffizienten werden geschätzt

Modellvalidierung (Qualität des Modells)

• R, R^2,
• F-Test des Gesamtmodells
• T-Test der einzelnen Koeffizienten

Prognose

• Kriterium vorhersagen
• Range beachten

Modell beurteilen, Residualanalyse, Modellverfeinerung, Modellvergleich, Variablenauswahl etc.

• Multikollinearitätsdiagnose
• Cooks Distance und Mahalanoby
• Jede Veränderung betrifft das Gesamtsystem
• Stepwise
• Wechselwirkungen (Interaktionsterme) als Prädiktoren

(Visualisierung).

F-Test als Omnibus-Test

Omnibus F-Test (F-statistic) prüft Hyp., dass alle Regressionskoeffizienten gleich 0 sind. bzw. ob durch die Vorhersage-Linearkombination ein signifikanter Anteil der Varianz am Kriterium erklärt wird.
bzw. H₀: R² ist 0

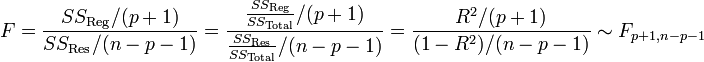
R² bzw. corrected R²

Multiple R-squared: Anteil der Varianz des Kriteriums, der durch die Kombination der Prädiktoren gebunden/erklärt wird.
Adjusted R-squared: rechnet R-squared so um, dass die Anzahl der erklärenden Terme im Modell berücksichtigt wird.
adjusted R-squared steigt im Gegensatz zu R-squared nur, wenn der neue Term das Modell um mehr als durch Zufall erwartet verbessert.
adjusted R-squared kann negativ sein und ist immer <= R-squared.

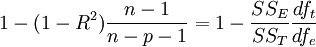
p Anzahl der Regressore im linear Model (ohne constant), n ist sample-size.

Moderatorvariable

Eine Moderatorvariable (oder kurz: Moderator) bezeichnet in der Statistik eine Variable C, von der abhängt, wie der Effekt einer Variable A auf eine andere Variable B ausfällt. Statistisch ein ein Interaktionseffekt.

Mediation

Mediatorvariable ist eine (dritte) Variable, die den beobachteten Zusammenhang zwischen Prädiktor und Kriterium erklärt (verändert, z. B. auch verschwinden läßt).

 

Supressor

Eine Suppressorvariable ist eine Variable, die den Vorhersagebeitrag einer (oder mehrer) anderer Variablen erhöht, indem sie irrelevante Varianzen unterdrückt. (Bortz, 1999, S.444)

• Die Supressorvariable korreliert nicht oder nur sehr gering mit dem Kriterium. Erkennbar in Korrelationsmatrix mit dem Kriterium, den Prädiktoren und den möglichen Supressorvariablen.
• Die mögliche Supressorvariable korreliert mit einem der anderen Prädiktoren sehr deutlich, ablesbar ebenfalls in obiger Korrelationsmatrix.
• Das Inkrement (bzw. das Dekrement) ist größer als der einfache Determinationskoeffizient. (Das Inkrement ist der Zuwachs im R^2, wenn das Modell um einen Prädiktor erweitert wird, das Dekrement die Differenz im R^2, wenn das Modell um einen Prädiktor verringert wird. Der einfache Determinationskoeffizient ist der quadrierte bivariate Korrelationskoeffizient des Prädiktors mit dem Kriterium).

Multikollinearität:

• Indices: VIF (Variance Inflation Factor)
  
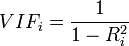
  und
• Toleranz
  
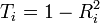
  Der Index i läuft über die Prädiktoren.
• VIF = 1 / Toleranz
• Die Indices werden gebildet auf Basis der multiplen Korrelation eines Prädiktors mit dem Rest der Prädiktoren. Inwieweit lässt sich ein Prädiktor aus den anderen vorhersagen.
• Daumenregel: Wenn der VIF 10 ( bzw. 5) überschreitet oder aber die Toleranz 0.1 bzw. Tol 0.2  unterschreitet gibt es Probleme mit Kollinearität im Pool der Prädiktoren. Die extremeren Werte stammen aus Everitt (2010) und sehen die Multikollinearitätsproblematik erst später als die Empfehlungen z. B. aus Wikipedia.

Residualanalyse

visuell in Scatterplot suchen nach Besonderheiten (Hinweise auf z. B. quadratische Reste, Varianzungleichheiten, Ausreißer)

Residuen mit QQ-Plot auf Normalverteilung überprüfen

quantitative Ausreißerkontrolle

standardisierte Residuen
Residuen werden durch die Standardabweichung geteilt (alle durch dieselbe). n ist Anzahl der Beobachtungen, m ist Anzahl der Parameter. (ev. auch n - m - 1 im Nenner weil Schätzer)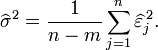

studentisierte Residuen
Residuen werden durch einen Schätzer der lokalen Standardabweichung geteilt (n und m s. o., h ist leverage)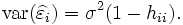

Leverage (Hebelwert)
Diagonalelemente der Hat-Matrix.
Hat-Matrix mappt die Kriterien auf die vorhergesagten Werte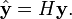

mit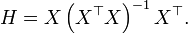

Jede vorhergesagte y^ kann als eine Linearkombination der Kriterien y_i dargestellt werden. Der Koeffizient der Beobachtung y_i, das ist h_ii, wir die Leverage dieser Beobachtung genannt (Diagonale). Je größer h_ii desto größer der Beitrag von y_i zu y_i*.
Leverage-Werte schwanken zwischen 0 und 1:  0 <= hii <= 1
Die Anzahl der leverages ist p, die Anzahl der Parameter des Regressionsmodells (Anzahl der Prädiktoren + 1 (Konstante))
Leverage kann als Distanzmaß der Beobachtung zum Zentrum aller Beobachtungen interpretiert werden.

 

Cook's distance: Einfluss eines Falles auf die Parameterschätzung des Gesamtmodells.
Misst den Effekt, den die Herausnahme dieser Person auf das Modell haben würde. Je höher der Wert, desto höher der Einfluss dieser Beobachtung. In die Cook's distance geht die Leverage als Paramter ein, außerdem die Anzahl der Parameter und der Residualwert der Beobachtung. MSE is the mean square error of the regression model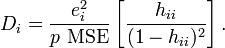

Ein Wert größer 1 heisst, dass diese Beobachtung einen unverhältnismäßig großen Einfluss hat (Empfehlung Everitt, 2010).
Andere Empfehlung: Cook's distance > 4 / n, wobei n die Anzahl der Beobachtungen ist (Quelle Wikipedia: http://en.wikipedia.org/wiki/Cook%27s_distance)

Mahalanobis-Distanz. Man kann sich vorstellen, dass die unabhängigen (i.allg. korrelierten) Variablen (in der Gleichung) einen mehrdimensionalen Raum beschreiben, in dem jede Beobachtung als Punkt eingezeichnet werden kann. Außerdem kann ein Punkt eingezeichnet werden, der die Mittelwerte all dieser Variablen repräsentiert (der Schwerpunkt dieser "Punktwolke" von Beobachtungen). Dieser "Mittelpunkt" wird auch der Zentroid genannt. Die Mahalanobis-Distanz ist der Abstand einer Beobachtung vom Zentroid. Dabei ist zu beachten, dass bei korrelierten Variablen die Achsen im Plot nicht-orthogonal zueinander sind, d.h., sie stehen nicht im rechten Winkel zueinander. In diesem Fall sind die einfachen Euklidischen Distanzen kein geeignetes Abstandsmaß, während die Mahalanobis-Distanzen die Korrelationen der Variablen adäquat berücksichtigen. Die Mahalanobis-Distanz liefert somit einen Anhaltspunkt, ob eine Beobachtung im Hinblick auf die unabhängigen Variablen als Ausreißer anzusehen ist oder nicht.

Modellanpassung

• Jede Veränderung am Modell verändert das Gesamtgefüge, beispielsweise auch das Verhältnis der Wichtigkeit von Prädiktoren. Daher Veränderungen in Einzelschritten und jeden Schritt prüfen
• Sparsamere Modelle. Ziel ist, eine gewisse Vorhersagequalität mit so wenig Prädiktoren zu erreichen, wie möglich.
• Modellbewertung und Modellvergleich:
  AIC (Akaike's information criterion) wie in Everitt(2010) zwischen den Alternativmodellen vergleichen und minimieren.
• Stepwise Regression. Forward and backward.
• Für die Prädiktoren-Selektion werden Veränderungen des F-Wertes benutzt (F to enter, F to remove)

 

Hintergrund

(aus Statistica Hilfe)

Die konkreten Berechnungen zur Lösung der Regressionsprobleme können kompakt und bequem mittels der Matrix-Schreibweise ausgedrückt werden. Es mögen n beobachtete Werte für Y und n damit zusammenhängende beobachtete Werte für jede der k verschiedenen X-Variablen geben. Dann bezeichnen Yi, Xik bzw. ei die i-te Beobachtung der Variablen Y, die i-te Beobachtung einer jeden X-Variablen bzw. den unbekannten i-ten Residualwert. Fasst man diese Größen in Matrizen zusammen, so erhält man: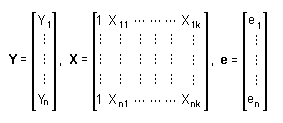



Das Modell der multiplen Regression kann dann in Matrix-Schreibweise wie folgt ausgedrückt werden:

Y = Xb + e

Hierbei ist b ein Spaltenvektor mit 1+k Elementen: 1 für die Konstante und k für die unbekannten Regressionskoeffizienten. Das Ziel der multiplen Regression besteht, wie bereits beschrieben, in der Minimierung der Summe der quadrierten Residuen. Die Regressionskoeffizienten, die diese Bedingung erfüllen, findet man, indem man die folgenden Gleichungen löst:

X'Xb = X' Y

Sind die X -Variablen linear unabhängig (d. h., sie sind nicht redundant und führen auf eine X'X -Matrix mit vollem Rang), gibt es eine eindeutige Lösung für diese Gleichungen. Werden beide Seiten der Gleichung von links mit der Inversen von X'X multipliziert, so ergibt dies:

(X'X)-1X'Xb = (X'X)-1X' Y

oder

b = (X'X)-1X' Y

Dieses Ergebnis ist im Hinblick auf seine Einfachheit und Allgemeingültigkeit sehr günstig. In Bezug auf die Einfachheit drückt es die Lösung für die Regressionsgleichung in Begriffen von nur zwei Matrizen (X und Y) sowie drei Grundoperationen für Matrizen aus: erstens die Matrixtransposition (Austausch der Elemente der Reihen und Spalten einer Matrix), zweitens die Matrixmultiplikation (Berechnung der Summe von Produkten der Elemente für jede Zeilen- und Spaltenkombination bei zwei verkettbaren (multiplizierbaren) Matrizen) und drittens die Matrix-Inversion (Auffinden der reziproken Matrix). Letzteres ist eine Matrix, die die folgende Bedingung erfüllt:

A-1AA = A

für die Matrix A.

Die Mathematiker (und Statistiker) haben sich sehr lange bemüht, um eine befriedigende Methode für die Lösung von linearen Kleinste-Quadrate-Regressionsgleichungen zu entwickeln. Aber die Bemühungen haben sich letztlich ausgezahlt, denn man kann sich kaum eine einfachere Lösung vorstellen.

Im Hinblick auf die Allgemeingültigkeit des Modells der multiplen Regression gibt es nur in zweierlei Hinsicht nennenswerte Beschränkungen. Erstens kann es nur für die Analyse einer einzigen abhängigen Variablen genutzt werden und zweitens liefert es keine Lösung für die Regressionskoeffizienten, wenn die X -Variablen nicht linear unabhängig sind und die Inversion von X'X folglich nicht möglich ist. Diese Beschränkungen können aber überwunden werden. Dies führt zur Transformation des Modells der multiplen Regression in das Allgemeine Lineare Modell ALM.

 

Aufgaben