loesungsansatz
Lösungsansatz
[noch unfertig - wird in der nächsten Zeit weiter aktualisiert.]
[Die hier gezeigten Ansätze sind beispielhaft. Es mag deutlich verschiedene geben, die ebenso richtig sind.]
Vorüberlegungen:
Die Erfassung der Merkfähigkeit erfolgt durch einen Test mit Messwerten zwischen 0 und 100 Punkten. Obwohl keine näheren Angaben zum Datenniveau gemacht wurden, gehen wir von Intervalldatenniveau aus, vor allem, da sich der Score aus vielen Einzeltestwerten zusammensetzt. Ausserdem sind Messwerte über psychologische Leistungsindices vielfach normalverteilt. Dies soll später an den Daten überprüft werden, soll aber zunächst für die Auswertungsplanung angenommen werden.
Da, wie bei Trainingsevaluationen üblich, ein Leistungsmaß mehrfach erhoben wurde, handelt es sich grundsätzlich um eine Art von Messwiederholungsdesign. Dies hat Implikationen auf die Beurteilung der Daten z. B. hinsichtlich der Abhängigkeit der Messwerte pro Person bzw. hinsichtlich der Wahl der Freiheitsgrade, mit denen die statistischen Tests durchgeführt werden.
Es wurden 3 Gruppen untersucht, wovon eine Gruppe als Warte-Kontrollgruppe fungiert. Diese soll den 'natürlichen' Verlauf ohne Intervention abschätzen lassen, wobei bereits die mehrfache Erhebung der Behaltensleistung Auswirkungen haben könnte. Ein Vergleich dieser Gruppe mit den andern beiden Trainingsgruppen lässt mich also den Effekt der Trainings abschätzen, wenn nicht Alternativerklärungen zum tragen kommen. Die Bemerkung, die Gruppen seien nach vielerlei Variablen wie Geschlecht, Alter, sozioökonomischem Status etc. vergleichbar, muss im vorgegebenen Kontext ausreichen, um Konfundierungen auszuschließen, da die Variablen nicht im Datensatz enthalten sind und somit eine eigene Überprüfung unmöglich ist.
Glücklicherweise sind die Gruppen gleich groß, so dass keine zusätzlichen Abhängigkeiten aufgrund unterschiedlicher Gruppengrößen in eventuellen varianzanalytischen Designs zu befürchten sind. Dies würde sonst die Wahl der Art der Quadratsummenbildung beeinflussen.
Trainingswirksamkeit
Als ersten Teilauftrag will die Brain-Fit GmbH von Ihnen wissen, ob ihr Gedächtnistraining wirksam ist. Wir beginnen mit einer Visualisierung der mittleren Behaltensleisung unmittelbar vor und nach der Trainingswoche.
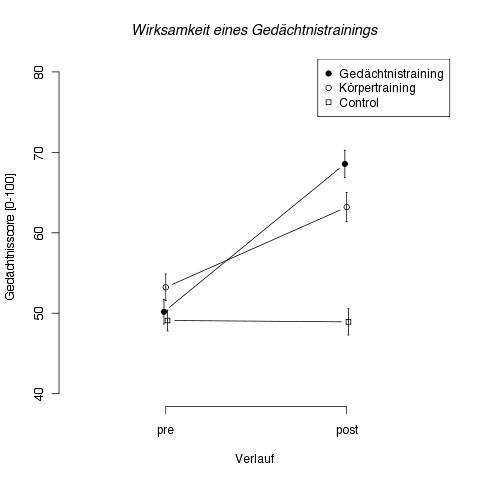
Bereits deskriptiv/grafisch ist klar zu erkennen, dass sich die Mittelwerte der beiden Trainingsgruppen erhöhen, während die Kontrollgruppe auf nahezu auf ihrem Ausgangsniveau bleibt. Alle Änderungen gehen deskriptiv in die erwartete Richtung. Zum Trainingsstart scheint es keine bedeutsamen Unterschiede zwischen den Gruppen zu geben. Allerdings fehlt eine statistische Absicherung.
Ein mindestens unmittelbare (kurzfristige) Verbesserung der Behaltensleistung durch das Brain-Fit-Training müßte sich durch sig. höhere Behaltenswerte (im Mittel) der Trainingsgruppe im Vergleich zur Kontrollgruppe zeigen. Darüber hinaus müsste sichergestellt sein, dass die relevanten Gruppen sich vor dem Training nicht mehr als nur zufällig unterscheiden. Eine statistische Absicherung könnte z. B. mittels zweier T-Tests zwischen Gedächtnistrainingsgruppe und KG zum Zeitpunkt pre und post erfolgen, sowie durch ein varianzanalytisches Design (2 Gruppen * pre/post) in dem sich eine signifikante Wechselwirkung zeigen müsste. Das Alpha-Niveau beim Überprüfen des "Nicht-Unterschieds" zum Ausgangspunkt sollte höher gewählt werden (z. B. 10% oder 20%) um den Beta-Fehler zu verringern. Alle drei Effekte müßten gegeben sein, um dem Training eine Wirksamkeit bescheinigen zu können (Testplanung).
R-Code und Ergebnisse zu diesem Ansatz:
>
> d.r <- read.delim(file="http://www.psych.uni-goettingen.de/mat/mv/brain-fit-r.txt")
>
> # T-Test Brain-Fit-Gruppe vs KG, Zeitpunkt pre
> t.test(d.r$score[d.r$group == 'gt' & d.r$tt == 'pre'], d.r$score[d.r$group == 'kg' & d.r$tt == 'pre'])
Welch Two Sample t-test
data: d.r$score[d.r$group == "gt" & d.r$tt == "pre"] and d.r$score[d.r$group == "kg" & d.r$tt == "pre"]
t = 0.5413, df = 95.741, p-value = 0.5896
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.883554 5.045554
sample estimates:
mean of x mean of y
50.1824 49.1014
>
> # T-Test Brain-Fit-Gruppe vs KG, Zeitpunkt post
> t.test(d.r$score[d.r$group == 'gt' & d.r$tt == 'post'], d.r$score[d.r$group == 'kg' & d.r$tt == 'post'])
Welch Two Sample t-test
data: d.r$score[d.r$group == "gt" & d.r$tt == "post"] and d.r$score[d.r$group == "kg" & d.r$tt == "post"]
t = 8.3326, df = 97.831, p-value = 4.976e-13
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
14.95932 24.31228
sample estimates:
mean of x mean of y
68.5638 48.9280
>
> # VA Design Pre-Post * Gruppe: Die unmittelbare Wirkung, nur Brain-Fit gegen KG
> # Datensatz "bauen"
> d.prepost <- d.r[151:450,]
> d.2prepost <- d.prepost[d.prepost$group != 'sp',]
> d.2prepost$tt <- factor(d.2prepost$tt)
> m.2prepost = aov(score ~ (group*tt) + Error(vp/tt) + (group), data=d.2prepost)
> summary(m.2prepost)
Error: vp
Df Sum Sq Mean Sq F value Pr(>F)
group 1 5364.8 5364.8 25.308 2.214e-06 ***
Residuals 98 20774.1 212.0
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: vp:tt
Df Sum Sq Mean Sq F value Pr(>F)
tt 1 4144.1 4144.1 155.99 < 2.2e-16 ***
group:tt 1 4303.5 4303.5 161.99 < 2.2e-16 ***
Residuals 98 2603.5 26.6
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
Der T-Test Gedächtnistrainingsgruppe - KG zum Zeitpunkt prä ist nicht signifikant (t = 0.54, df = 95.741, p-value = 0.59). Auch bei hoch gewähltem Alpha (= 0.2) liegt der p-Wert deutlich höher, so dass man nicht von einem systematischen Gruppenunterschied zum Trainingsstart ausgehen kann, die Gruppen können also als vergleichbar gelten. Am Ende des Trainings ist das völlig anders. Die Trainingsgruppe hat einen signifikant höheren Wert in der Behaltensleistung als die Kontrollgruppe (t = 8.33, df = 97.831, p-value <= 0.001).
Ebenfalls erwartungskonform zeigt die zweifaktorielle Varianzanalyse eine hochsignifikante Wechselwirkung, was belegt, dass sich die beiden Gruppen in der Zeit zwischen pre und post völlig verschieden entwickelt haben (F=161.99, df1=1, df2=98, p<=0.001, s.).
[hier nicht eingefügt sind die Überprüfung der Normalverteilungsvoraussetzung bzw. die deskriptive Analyse der Daten auf Verteilungsbesonderheiten.]
[ alternativ könnte man natürlich mit Statistica dieselben Berechnungen durchführen ]
Frage 2: Das beste Training?
Die Aussage "Die mit unserem Verfahren trainierten Personen erreichen klar die höchsten Werte" soll hier so interpretiert werden, dass die mit Brain-Fit trainierte Personengruppe einen signifikant höheren Mittelwert nach dem Training hat, als die körperlich traininerte Gruppe und selbstverständlich auch signifikant über dem Mittelwert der Kontrollgruppe liegt.
[statistischer Beleg beispielsweise durch entsprechende multiple T-Tests mit entsprechender Testplanung oder via VA und geplanten Vergleichen o. ä. Alles sollte gesehen werden im (grafischen) Vergleich mit den Werten vor Trainingsbeginn.]
Stabilität
Durch die Öffentlichkeitsarbeit der Brain-Fit GmbH werden die 'Grauen Panther' (Partei, zur Interessensvertretung von Senioren) auf das Training aufmerksam. Auf Einladung des Bundesvorstandes der 'Grauen Panther' stellen Sie auf Anregung und mit Zustimmung Ihres Auftraggebers Ihre Evaluationsergebnisse vor.
Sie werden explizit und kritisch nach der Stabilität der Trainingserfolge von "Brain-Fit©" befragt und zeigen die folgende Grafik, die die Entwicklung der Gedächtnistest-Werte in den 3 Wochen nach Trainingsende zeigt.
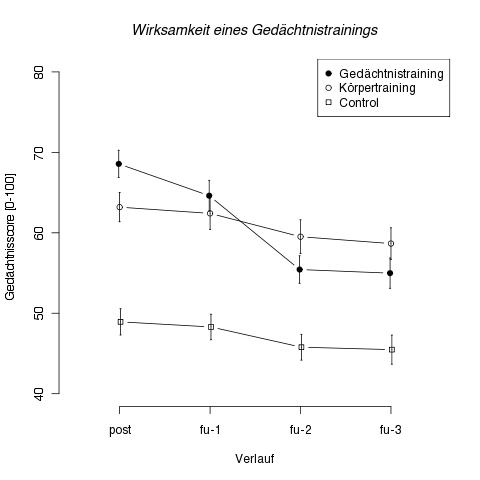
Der wissenschafliche Beauftragte der Partei kritisiert, dass nach drei Wochen ja das körperliche Training die besseren Gedächtniswerte ergäbe. Die Wirksamkeit des Gedächtnistrainings sei also klar wiederlegt.
R: Test der letzten beiden Messzeitpunkte über die drei Gruppen
> ##dev.off()
> # fu2 und fu3 (Langzeiteffekt)
> d.fu2.fu3 <- d.r[601:900,]
> d.fu2.fu3$tt <- factor(d.fu2.fu3$tt)
> m.fu2.fu3 = aov(score ~ (group*tt) + Error(vp/tt) + (group),data=d.fu2.fu3)
> summary(m.fu2.fu3)# und die Mittelwerte dazu
Error: vp
Df Sum Sq Mean Sq F value Pr(>F)
group 2 9598 4798.8 15.935 5.45e-07 ***
Residuals 147 44269 301.2
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: vp:tt
Df Sum Sq Mean Sq F value Pr(>F)
tt 1 21.5 21.467 0.5256 0.4696
group:tt 2 4.0 2.012 0.0493 0.9519
Residuals 147 6003.7 40.841
R: Test der letzten beiden Messzeitpunkte zwischen den beiden Trainingsgruppen
> # fu2 und fu3 (Langzeiteffekt) ohne KG
> d.fu2.fu3.no.kg <- d.fu2.fu3[d.fu2.fu3$group != 'kg',]
> d.fu2.fu3.no.kg$tt <- factor(d.fu2.fu3.no.kg$tt)
> m.fu2.fu3.no.kg = aov(score ~ (group*tt) + Error(vp/tt) + (group),data=d.fu2.fu3.no.kg)
> summary(m.fu2.fu3.no.kg)
Error: vp
Df Sum Sq Mean Sq F value Pr(>F)
group 1 752 751.67 2.2693 0.1352
Residuals 98 32461 331.24
Error: vp:tt
Df Sum Sq Mean Sq F value Pr(>F)
tt 1 21.1 21.145 0.5898 0.4443
group:tt 1 2.0 2.030 0.0566 0.8124
Residuals 98 3513.1 35.847
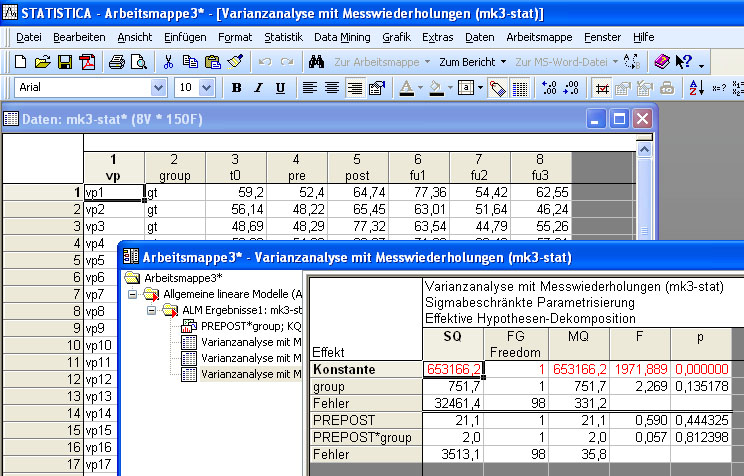
Statistica: Test der letzten beiden Messzeitpunkte über die drei Gruppen
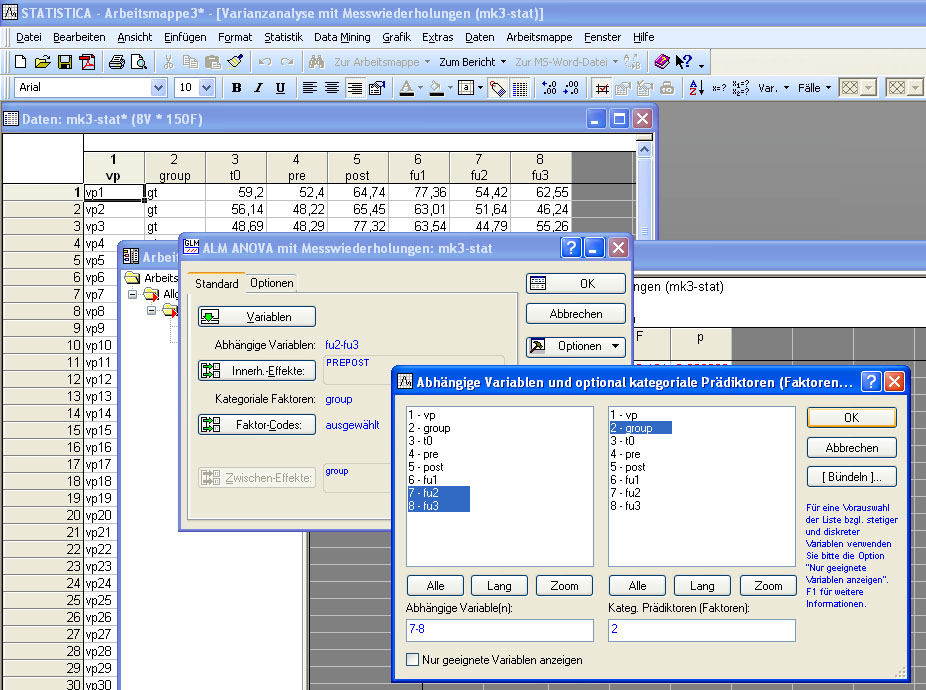
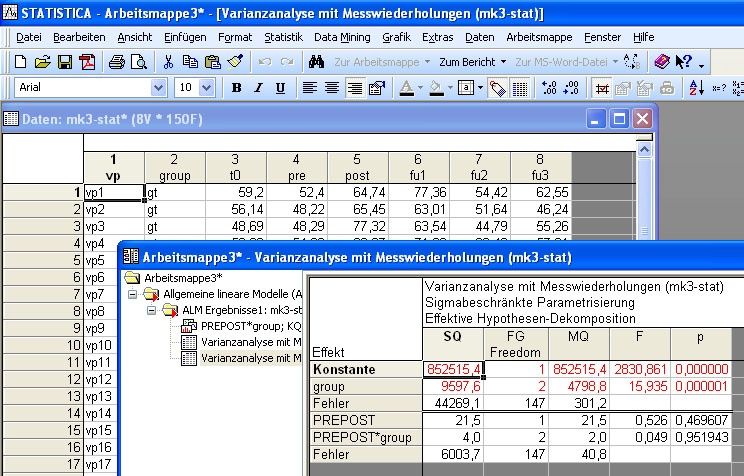
Statistica: Test der letzten beiden Messzeitpunkte zwischen den beiden Trainingsgruppen
[weitere Kommentare und Interpretationen hinsichtlich der Fragestellungen fehlen und folgen noch]